La sphère est dans l’œuf !
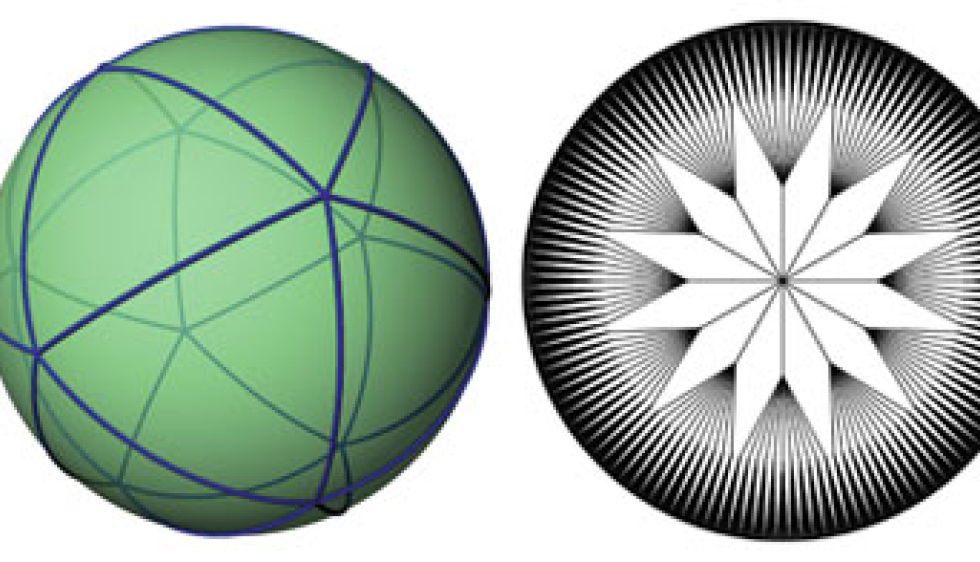
Pour classer ensemble les surfaces qui se ressemblent, l’arithmétique se révèle aussi utile que la géométrie.
Regardez un point sur une boule à la loupe. De près. De très près. Si votre loupe est assez puissante, vous ne verrez plus la boule en entier, seulement la zone autour du point. Et vous ne pourrez même plus dire qu’il s’agit d’une boule, car vous ne verrez plus ses courbes, juste une zone “plate” autour du point de départ. En mathématiques, c’est ce qui caractérise les variétés : ce sont des surfaces qui, autour de chacun de leurs points, peuvent être assimilées à un plan. On compte parmi elles la sphère mais aussi les tores, qu’ils aient un trou – c’est un pneu – deux trous – un huit en volume – ou plus encore.
Recouvrir de triangles
« Un des objectifs de l’homologie et de la cohomologie, c’est de voir si deux variétés se ressemblent, explique Xavier Caruso, chercheur dans l’équipe de géométrie algébrique, à l’Irmar(1), si l’on peut passer de l’une à l’autre juste en les déformant. » Si vous écrasez une sphère, vous obtiendrez un œuf. Par contre, à partir de la même sphère, vous n’obtiendrez jamais un pneu sans la casser ! « Pour le vérifier, l’homologie définit des invariants. Des caractéristiques qui sont toujours les mêmes sur les surfaces semblables. Par exemple, si l’on recouvre la sphère ou l’œuf de petits triangles, le calcul nombre de sommets + nombre de faces – nombre d’arêtes sera toujours égal à 2. Par contre, sur le tore, le même calcul sera égal à zéro. »
Cela donne une première information et fonctionne bien pour les variétés les plus simples citées plus haut. Mais quand elles se compliquent, il faut utiliser d’autres boîtes à outils. Xavier Caruso s’intéresse à deux d’entre elles : la cohomologie cristalline, qui a été développée à Rennes, par Pierre Berthelot en 1974. Et la cohomologie étale. « La seconde donne énormément d’informations géométriques et arithmétiques, grâce aux groupes de Galois (lire ci-dessous) notamment. La première est plus simple d’utilisation. Pourtant, elle recèle les mêmes informations, car il existe des équivalences entre les deux. » Cela peut s’avérer utile. Par exemple, les recherches sur le cryptage d’informations électroniques (lire ci-contre) ont besoin d’une formule de la cohomologie étale. Mais comme elle est difficile à calculer, il est plus simple de passer par la voie cristalline.
« Aujourd’hui, j’essaye de voir si les formules de passage d’une boîte à outils à l’autre, qui ont été démontrées mathématiquement, sont applicables sur des cas concrets, sur ordinateur. » Or les machines ont des limites. Par exemple, elles ne peuvent pas traiter tous les nombres réels, certains ont une infinité de chiffres après la virgule. « Il faut savoir où tronquer, quelles approximations faire avec quelles conséquences... » L’application est parfois aussi compliquée que la théorie.
(1) Irmar : Institut de recherche mathématique de Rennes.
Xavier Caruso
02 23 23 58 92
xavier.caruso [at] normalesup.org (xavier[dot]caruso[at]normalesup[dot]org)
TOUT LE DOSSIER
du magazine Sciences Ouest